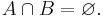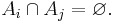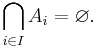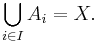Disjoint sets

In mathematics, two sets are said to be disjoint if they have no element in common. For example, {1, 2, 3} and {4, 5, 6} are disjoint sets.^[1]

Explanation

Formally, two sets A and B are disjoint if their intersection is the empty set, i.e. if

$A\cap B = \varnothing.\,$

This definition extends to any collection of sets. A collection of sets is pairwise disjoint or mutually disjoint if, given any two sets in the collection, those two sets are disjoint.

Formally, let I be an index set, and for each i in I, let A_i be a set. Then the family of sets {A_i : i ∈ I} is pairwise disjoint if for any i and j in I with i ≠ j,

$A_i \cap A_j = \varnothing.\,$

For example, the collection of sets { {1}, {2}, {3}, ... } is pairwise disjoint. If {A_i} is a pairwise disjoint collection (containing at least two sets), then clearly its intersection is empty:

$\bigcap_{i\in I} A_i = \varnothing.\,$

However, the converse is not true: the intersection of the collection {{1, 2}, {2, 3}, {3, 1}} is empty, but the collection is not pairwise disjoint. In fact, there are no two disjoint sets in this collection.

A partition of a set X is any collection of non-empty subsets {A_i : i ∈ I} of X such that {A_i} are pairwise disjoint and

$\bigcup_{i\in I} A_i = X.\,$

References

^ "Stats: Probability Rules". People.richland.edu. http://people.richland.edu/james/lecture/m170/ch05-rul.html. Retrieved 2011-11-08.

Weisstein, Eric W., "Disjoint Sets" from MathWorld.

Disjoint sets

Explanation

See also

References